[백준] 11401번 이항계수3

Divide & conquer 정복기 - 1

문제

분할정복

문제를 나눌 수 없는 경우까지 나누어서 풀면서 다시 합병하여 문제의 답을 얻는 알고리즘이다.

페르마의 소정리(Fermat’s littls theorem)

\(소수p와 정수a에 대해서 a^p \equiv a(mod p)를 만족할때, 만약 a, p가 서로소이면 a^(p-1) \equiv 1(mod p)를 만족한다.\)

문제 풀이

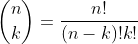
이므로 이를 활용하면 분할 정복을 이용한 거듭제곱을 적용시킬 수 있다.

---

전체코드 자세히 보기

#include <iostream>
#include <algorithm>
#include <vector>
#define mod 1000000007
using namespace std;
//분할 정복을 이용한 거듭제곱
long long int solution(long long int a, long long int b){ 
    if(b == 1)
        return a % mod;
    long long int tmp = solution(a, b / 2);
    if(b % 2 == 0)
        return (tmp * tmp) % mod;
    else
        return (((tmp * tmp) % mod) * a) % mod;
}
int main(void){
    cin.tie(NULL);
    cout.tie(NULL);
    ios::sync_with_stdio(false);
    int n, k;
    cin >> n >> k;
    vector<long long int> memo(4000001, 0);
    memo[0] = 1;
    for(int i = 1; i <= n; i++){
        memo[i] = (memo[i - 1] * i) % mod;
    }
    if(n == k || !k){
        cout << "1\n";
        return 0;
    }
    // temp = (n-k)!k!, answer = n! / temp
    long long int temp = (memo[k] * memo[n - k]) % mod;
    long long int answer = (memo[n] * solution(temp, mod - 2)) % mod; 
    cout << answer << "\n";
    return 0;
}

---

문제 결과

문제 출처 https://www.acmicpc.net/problem/11401