[백준] 1991번 트리 순회

백준 트리 순회 문제 풀이

이진트리

이진 트리는 각 노드가 최대 두 개의 자식 노드를 갖는 트리 구조를 말한다. 이진 트리는 컴퓨터 과학에서 가장 기본적인 자료 구조 중 하나로, 다양한 문제에 활용된다.

이진 트리의 순회

이진 트리의 모든 노드를 방문하는 방법을 순회(traversal)라고 한다. 이진 트리의 순회에는 크게 세 가지 방법이 있다.

• 전위 순회 (Preorder Traversal) : 루트 노드 -> 왼쪽 서브 트리 -> 오른쪽 서브 트리 순으로 방문
• 중위 순회 (Inorder Traversal) : 왼쪽 서브 트리 -> 루트 노드 -> 오른쪽 서브 트리 순으로 방문
• 후위 순회 (Postorder Traversal) : 왼쪽 서브 트리 -> 오른쪽 서브 트리 -> 루트 노드 순으로 방문

이진 트리의 순회는 대부분 재귀로 구현된다.

// 전위 순회
void static preorder(Tree* root) {
	if(root){
		cout << root -> data << "\n";
		preorder(root -> left);
		preorder(root -> right);
}

// 중위 순회
void inorder(Tree* root) {
	if(root){
		inorder(root -> left);
		cout << root -> data << "\n";
		inorder(root -> right);
}

// 후위 순회
void postorder(Tree* root) {
	if(root){
		inorder(root -> left);
		inorder(root -> right);
		cout << root -> data << "\n";
}

이진 트리의 구현

이진 트리는 포인터를 이용해 구현할 수 있다. 각 노드는 데이터와 왼쪽 자식 노드, 오른쪽 자식 노드를 가리키는 포인터를 갖는다.

class Tree{
	int data;
    Tree *left;
    Tree *right;
};

PS코드

이진트리의 순회를 구현하는 가장 기본적인 백준문제를 풀면서 실제로 구현을 연습해볼 수 있다.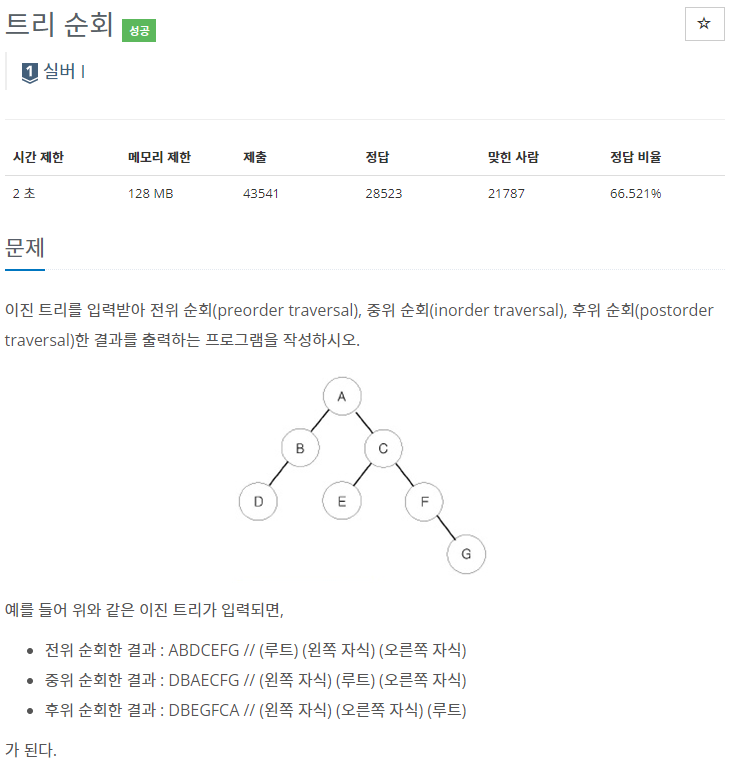

#include <bits/stdc++.h>
using namespace std;
class Tree{
    char root;
    Tree* left;
    Tree* right;
    public:
    	//노드 생성자
        Tree(){
            root = ' ';
            left = NULL;
            right = NULL;
        }
        //루트노드 설정
        void setRoot(char root){
            this -> root = root;
        }
        //왼쪽 서브 트리 설정
        void setLeft(Tree* left){
            this -> left = left;
        }
        //오른쪽 서브 트리 설정
        void setRight(Tree* right){
            this -> right = right;
        }
        //전위 순회
	    void static preorder(Tree* r) {
	    	if (r) {
	    		cout << r->root;
	    		preorder(r->left);
	    		preorder(r->right);
	    	}
	    }
    	//중위 순회
	    void static inorder(Tree* r) {
	    	if (r) {
	    		inorder(r->left);
	    		cout << r->root;
	    		inorder(r->right);
	    	}
	    }
    	//후위 순회
	    void static postorder(Tree* r) {
	    	if (r) {
	    		postorder(r->left);
	    		postorder(r->right);
	    		cout << r->root;
	    	}
	    }
};
int main(void){
    cin.tie(NULL);
    cout.tie(NULL);
    ios::sync_with_stdio(false);
    int n;
    cin >> n;
    Tree *tree = new Tree[n];
    for (int i = 0; i < n; ++i) {
        char root,left,right;
        cin >> root >> left >> right;
        if(root!='.')
            tree[(int)(root-'A')].setRoot(root);
        if (left != '.')
            tree[(int)(root - 'A')].setLeft(&tree[(int)(left - 'A')]); // 왼쪽서브트리 형성을 위한 입력
        else
            tree[(int)(root - 'A')].setLeft(NULL);
        if (right != '.')
            tree[(int)(root - 'A')].setRight(&tree[(int)(right - 'A')]); // 오른쪽서브트리 형성을 위한 입력
        else
            tree[(int)(root - 'A')].setRight(NULL);
    }
    Tree *root = &tree[0]; // 항상 A노드가 루트노드이므로
    Tree::preorder(root);
    cout << "\n";
    Tree::inorder(root);
    cout << "\n";
    Tree::postorder(root);
    cout << "\n";
}

참고자료

https://hongku.tistory.com/160 https://www.acmicpc.net/problem/1991