자료구조의 기본인 Segment tree를 사용하는 문제이다. Segment tree의 가장 기본인 문제!
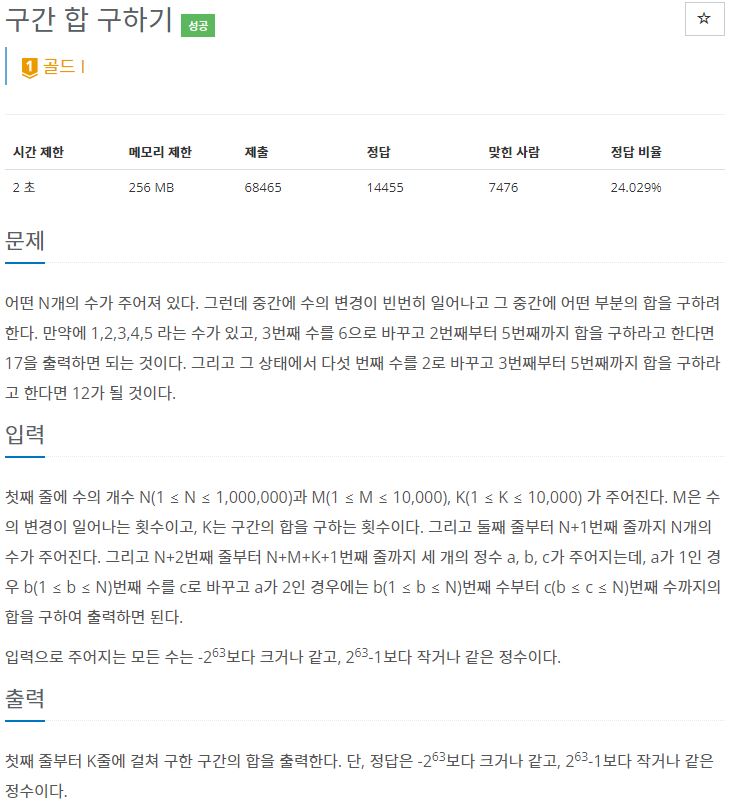
문제
문제 풀이
이번 문제는 segment tree의 기본문제로 해당문제가 segment tree라는 자료구조를 모른다면 풀이과정이 매우 복잡해질 수 있다.
Segment tree?
여러개의 데이터가 존재할 때 특정구간의 합이나, 최솟값, 최댓값, 곱등을 구하는데 사용하는 자료구조이다. 트리 종류중에 하나로 이진 트리의 형태, 특정구간의 합을 가장 빠르게 구할 수 있다는 장점이 있다.(시간 복잡도의 경우 Olog(n))
가장 이해하기 쉬운 예시로 배열이 주어졌을 때, 구해야하는 합의 구간이 여러가지 일 경우의 Segment tree를 사용하지 않게되면, 시간 복잡도가 O(n)이다. 그러나 Segment tree를 사용하게 되면 Olog(n)의 복잡도로 풀이 가능하다. 예시를 보면서 설명하겠다.
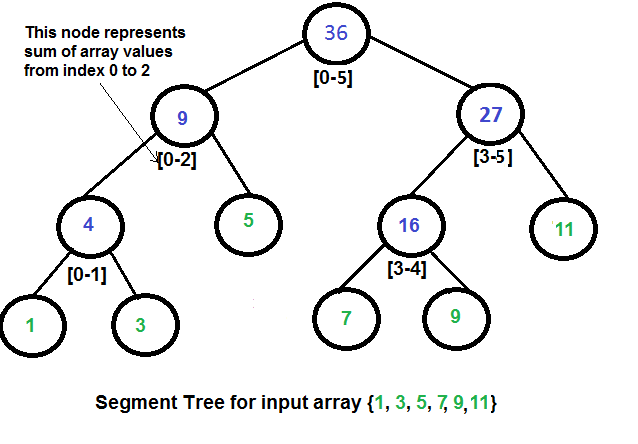
위의 그림은 arr[6] = {1, 3, 5, 7, 9, 11};의 Segment tree이다. 이때 node에는 합이 들어가 있는 것을 볼 수 있다. 이러한 Segment tree를 만들어 놓고, 만약 필요한 구간의 index가 2~4라고 예를 들면 5와 [3, 4]의 node값을 재귀로 찾아서 풀이 하면 된다. 이러한 코드를 나누어서 보여주겠다.
세그먼트 트리 구성에 주의 할 점
- 트리의 크기는 요소의 개수의 4배로 구성한다. 이유는 트리의 최대 node 갯수는 요소의 개수의 제곱이기 때문이다.
- 재귀로 풀이하는 것이 좋다. 이는 코드를 보면 확인할 수 있다.
main function
int main(void){
cin.tie(NULL);
cout.tie(NULL);
ios::sync_with_stdio(false);
int n, m, k;
cin >> n >> m >> k;
for(int i = 1; i <= n; i++)
cin >> arr[i];
init(1, n, 1); //segment tree 구하기
for(int i = 0; i < m + k; i++)
{
long long int a, b, c;
cin >> a >> b >> c;
if(a == 1)
{
long long int diff;
diff = c - arr[b];
arr[b] = c;
update(1, n, 1, b, diff); //배열의 element 교체로 인한 segment tree 업데이트
}
else if(a == 2)
{
cout << sum(1, n, 1, b, c) << "\n"; //구간합 결과 출력
}
}
}
main 함수의 경우 별다른 설명 없이도 알 수 있을 거라고 생각한다. 다만 문제에서 “입력으로 주어지는 모든 수는 -263보다 크거나 같고, 263-1보다 작거나 같은 정수이다.”라는 조건을 주의해서 풀이 해주어야 한다.
init function
long long int init(int start, int end, int node)
{
if(start == end)
return tree[node] = arr[start];
int mid = (start + end) / 2;
return tree[node] = init(start, mid, node * 2) + init(mid + 1, end, node * 2 + 1);
}
세그먼트 트리를 구성하는 함수의 경우에는 element를 그대로 리턴하는 부분과 재귀로 가는 부분으로 구성되어 있다. 이때 node 번호의 경우 현재 노드에서 node * 2, node *2 + 1한것으로 설정한다. 또한 구간을 나눌때 중간 부분으로 나누어야 한다.
sum function
long long int sum(int start, int end, int node, int left, int right)
{
if(right < start || left > end)
return 0;
if(left <= start && end <= right)
return tree[node];
int mid = (start + end) / 2;
return sum(start, mid, node * 2, left, right) + sum(mid + 1, end, node * 2 + 1, left, right);
}
합을 구하는 함수에서는 구하고자 하는 구간에 포함되어 있는 node는 재귀를 통해 더해주면 된다.
update function
void update(int start, int end, int node, int index, long long int change)
{
if(index < start || index > end)
return;
tree[node] += change;
if(start == end)
return;
int mid = (start + end) / 2;
update(start, mid, node * 2, index, change);
update(mid + 1, end, node * 2 + 1, index, change);
}
update 함수의 경우에는 변화가 있는 index와 차이값을 통해 segment tree에서 index가 포함된 node를 다시 바꿔주면 된다.
전체코드 자세히 보기
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;
vector<long long int> tree(1000005 * 4, 0);
vector<long long int> arr(1000005, 0);
long long int init(int start, int end, int node)
{
if(start == end)
return tree[node] = arr[start];
int mid = (start + end) / 2;
return tree[node] = init(start, mid, node * 2) + init(mid + 1, end, node * 2 + 1);
}
long long int sum(int start, int end, int node, int left, int right)
{
if(right < start || left > end)
return 0;
if(left <= start && end <= right)
return tree[node];
int mid = (start + end) / 2;
return sum(start, mid, node * 2, left, right) + sum(mid + 1, end, node * 2 + 1, left, right);
}
void update(int start, int end, int node, int index, long long int change)
{
if(index < start || index > end)
return;
tree[node] += change;
if(start == end)
return;
int mid = (start + end) / 2;
update(start, mid, node * 2, index, change);
update(mid + 1, end, node * 2 + 1, index, change);
}
int main(void){
cin.tie(NULL);
cout.tie(NULL);
ios::sync_with_stdio(false);
int n, m, k;
cin >> n >> m >> k;
for(int i = 1; i <= n; i++)
cin >> arr[i];
init(1, n, 1);
for(int i = 0; i < m + k; i++)
{
long long int a, b, c;
cin >> a >> b >> c;
if(a == 1)
{
long long int diff;
diff = c - arr[b];
arr[b] = c;
update(1, n, 1, b, diff); //배열의 element 교체로 인한 segment tree 업데이트
}
else if(a == 2)
{
cout << sum(1, n, 1, b, c) << "\n"; //구간합 결과 출력
}
}
}
문제 결과
문제 출처 https://www.acmicpc.net/problem/2042
참고 출처 https://m.blog.naver.com/ndb796/221282210534 https://yongj.in/data%20structure/Segment-Tree/
댓글남기기