C++ Segment Tree 정리
Segment tree?
여러개의 데이터가 존재할 때 특정구간의 합이나, 최솟값, 최댓값, 곱 등을 구하는 데 사용하는 자료구조이다. 트리종류중ㅇ에 하나로 이진 트리의 형태, 특정구간의 합을 가장 빠르게 구할 수 있는 장점이 있다. (시간 복잡도의 경우 Olong(N)이다.)
가장 이해하기 쉬운 예시로 배열이 주어졌을 떄, 구해야하는 합의 구간이 여러가지일 경우의 Segment tree를 사용하지 않게 된다면, 시간 복잡도는 O(N)이다. 그러나 Segment tree를 사용하면, Olog(n)의 복잡도로 풀이가 가능하다.
arr[6] = {1, 3, 5, 7, 9, 11};
이러한 배열을 segment tree로 표현하게 되면 아래와 같은 그림이 나온다.
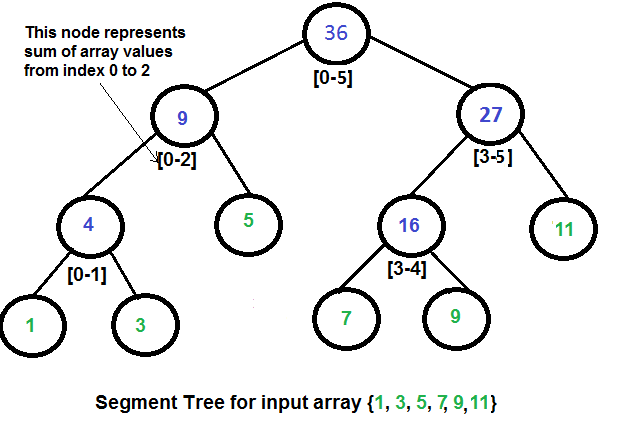이때 node에 합을 넣게 된다면, 필요한 구간 합을 구할 수 있다. 예를 들어 index값이 2~4에 해당하는 구간 합을 구하고자 할 때, a[2] 와 a[3] + a[4]에 해당하는 노드값의 합을 재귀의 형식으로 풀이할 수 있다.
segment tree 구성에서 주의 할 점
- 트리의 크기는 요소의 개수의 4배로 구성한다. 이유는 트리의 최대 node 갯수는 요소의 개수의 제곱이기 때문이다.
- 재귀로 풀이하는 것이 좋다.
이러한 segment tree를 이용한 백준의 구간 합 구하기 문제를 보면서 이해해보자!
main
int main(void){
cin.tie(NULL);
cout.tie(NULL);
ios::sync_with_stdio(false);
int n, m, k;
cin >> n >> m >> k;
for(int i = 1; i <= n; i++)
cin >> arr[i];
init(1, n, 1); //segment tree 구하기
for(int i = 0; i < m + k; i++)
{
long long int a, b, c;
cin >> a >> b >> c;
if(a == 1)
{
long long int diff;
diff = c - arr[b];
arr[b] = c;
update(1, n, 1, b, diff); //배열의 element 교체로 인한 segment tree 업데이트
}
else if(a == 2)
{
cout << sum(1, n, 1, b, c) << "\n"; //구간합 결과 출력
}
}
}
\(2^{63} 보다 크거나 같고, 2^{63} -1 보다 작거나 같은 정수이다\) 위와 같은 조건을 주의하자
init function
long long int init(int start, int end, int node)
{
if(start == end)
return tree[node] = arr[start];
int mid = (start + end) / 2;
return tree[node] = init(start, mid, node * 2) + init(mid + 1, end, node * 2 + 1);
}
세그먼트 트리를 구성하는 함수의 경우에는 element를 그대로 리턴하는 부분과 재귀로 가는 부분으로 구성되어 있다. 이때 node 번호의 경우 현재 노드에서 node * 2, node * 2 + 1한것으로 설정한다. 또한 구간을 나눌때 중간 부분으로 나누어야 한다.
sum function
long long int sum(int start, int end, int node, int left, int right)
{
if(right < start || left > end)
return 0;
if(left <= start && end <= right)
return tree[node];
int mid = (start + end) / 2;
return sum(start, mid, node * 2, left, right) + sum(mid + 1, end, node * 2 + 1, left, right);
}
합을 구하는 함수에서는 구하고자 하는 구간에 포함되어 있는 node는 재귀를 통해 더해주면 된다.
update function
void update(int start, int end, int node, int index, long long int change)
{
if(index < start || index > end)
return;
tree[node] += change;
if(start == end)
return;
int mid = (start + end) / 2;
update(start, mid, node * 2, index, change);
update(mid + 1, end, node * 2 + 1, index, change);
}
update 함수의 경우에는 변화가 있는 index와 차이값을 통해 segment tree에서 index가 포함된 node를 다시 바꿔주면 된다.
전체코드 보기
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;
vector<long long int> tree(1000005 * 4, 0);
vector<long long int> arr(1000005, 0);
long long int init(int start, int end, int node)
{
if(start == end)
return tree[node] = arr[start];
int mid = (start + end) / 2;
return tree[node] = init(start, mid, node * 2) + init(mid + 1, end, node * 2 + 1);
}
long long int sum(int start, int end, int node, int left, int right)
{
if(right < start || left > end)
return 0;
if(left <= start && end <= right)
return tree[node];
int mid = (start + end) / 2;
return sum(start, mid, node * 2, left, right) + sum(mid + 1, end, node * 2 + 1, left, right);
}
void update(int start, int end, int node, int index, long long int change)
{
if(index < start || index > end)
return;
tree[node] += change;
if(start == end)
return;
int mid = (start + end) / 2;
update(start, mid, node * 2, index, change);
update(mid + 1, end, node * 2 + 1, index, change);
}
int main(void){
cin.tie(NULL);
cout.tie(NULL);
ios::sync_with_stdio(false);
int n, m, k;
cin >> n >> m >> k;
for(int i = 1; i <= n; i++)
cin >> arr[i];
init(1, n, 1);
for(int i = 0; i < m + k; i++)
{
long long int a, b, c;
cin >> a >> b >> c;
if(a == 1)
{
long long int diff;
diff = c - arr[b];
arr[b] = c;
update(1, n, 1, b, diff); //배열의 element 교체로 인한 segment tree 업데이트
}
else if(a == 2)
{
cout << sum(1, n, 1, b, c) << "\n"; //구간합 결과 출력
}
}
}
문제 출처 https://www.acmicpc.net/problem/2042
참고 출처 https://m.blog.naver.com/ndb796/221282210534 https://yongj.in/data%20structure/Segment-Tree/
댓글남기기